4. 机器学习构成¶
预期收益
- ★ 机器学习基本概念及符号化
- ★ 机器学习流程本质, 在假设空间中, 应用机器学习算法找到一个在历史数据中上表现最佳的假设函数
时间成本
- 阅读 03 分钟
- 思考 05 分钟
4.1. 概念及符号化¶
信用卡申请案例
根据历史审核经验, 判断新的用户申请是否通过
- 目标, 银行根据申请信用卡的用户信息, 判断是否发卡
- 历史数据, 申请信息(年龄、性别、年收入、负责、工作年龄等)及对应审核是否发卡的结果
| 符号 | 含义 | 示例 |
|---|---|---|
| \(x\) | 输入特征 | 用户申请信息, \(x=[年龄, 性别, 年输入, \ldots]\) |
| \(y\) | 输出结果 | 用户申请是否通过, \(y=YES/NO\) |
| \(f\) | 目标函数(target function) | 审核结果和用户申请信息之间的关系, \(y=f(x)\) |
| \(\mathcal{h}\) | 假设函数(hypothesis) | 潜在可能的输入和输出之间的关系. 比如, \(\mathcal{h_1}\): 负债小于10w都能获取审核通过, 其它不通过 |
| \(\mathcal{H}\) | 假设空间,假设函数的集合 | 比如, \(\mathcal{H}=\{h_1, h_2, \ldots\}\) |
| \(\mathcal{D}\) | 训练数据, 历史经验数据 | 由历史用户信息和对应是否审核通过构成的集合. \(\mathcal{D}=\{(x_1, y_1), (x_2, y_2), \ldots\}\) |
4.2. 机器学习流程的数学本质¶
- 寻找输入和输出之间规律, 机器学习通常在给定的假设空间中找到一个最逼近目标函数的一个假设, 作为输入和输出之间的规律
- 如何判定找到的这个假设是最佳呢? 我们用历史数据来检查, 即在过去的数据中, 真实输出的结果和假设的结果最接近
- 找到最接近的假设的方法我们成为机器学习算法
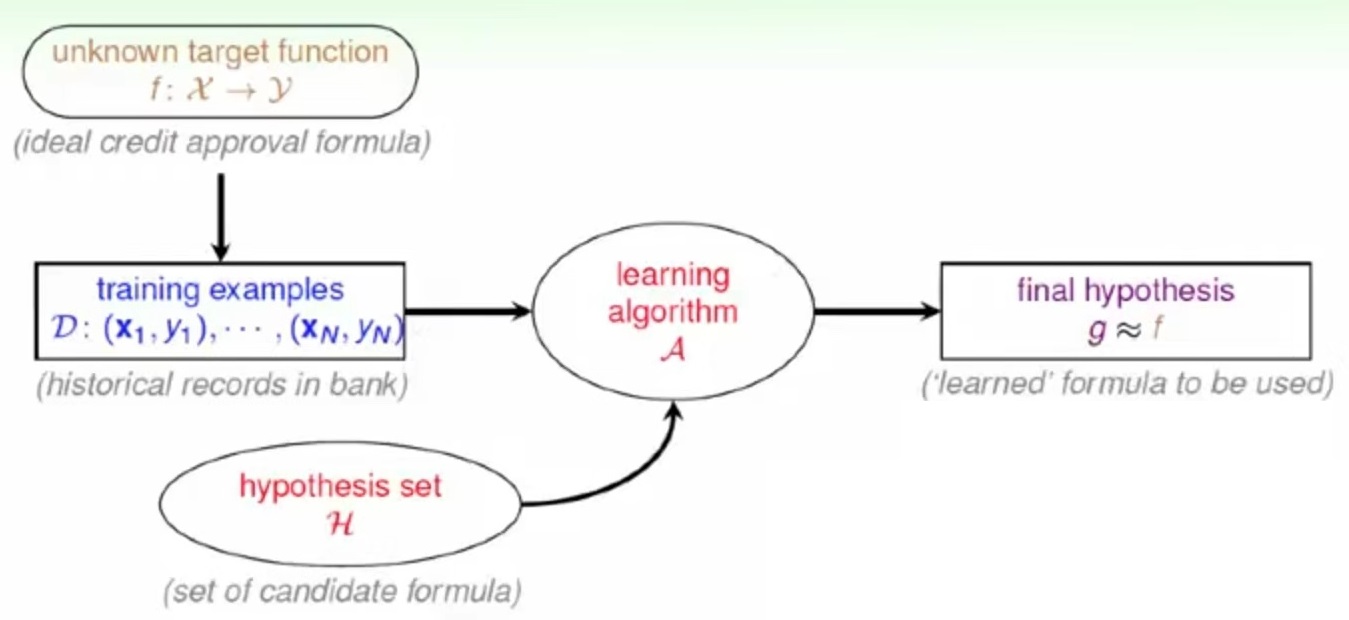
注解
- 什么样的历史数据才能保证, 选出的假设函数能够近似表示目标函数
- 足够多, 假如只有一条历史数据, 无法反应出输入和输出之间的一般规律
- 独立同分布, 样本之间没有相关性, 并且是来自同一分布, 表明数据可能含有相同的规律